汉诺塔：递归的基本原理与具体实现

汉诺塔(Tower of Hanoi)

汉诺塔我们都知道，一个源于印度古老传说的益智玩具，讲述的是在一个寺庙中有三根柱子，第一根上有着64个金盘，僧侣会以以下规则来将所有的金盘移到第三根柱子上：

1. 每次盘子移动次数只有一次
2. 小盘子永远在大盘子上面

当盘子全移动到第三根柱子上时，世界就会毁灭。

这个谜题曾被法国数学家 爱德华·卢卡斯 发扬成经典的汉诺塔问题，如今也成为了编程中经典的递归问题。

递归

基本原理

在编程中，递归的原理就是函数调用本身，这样的特性可以使得解决问题时将一个大问题被分解成若干个同样流程的小问题来实现。显著的简化了某些具有重复子问题结构的任务的实现方法。

递归的具体行为则是递与归，在自我调用的时候层层深入，直到壁点，随后逐层弹出，完成操作。

阶乘问题

许多文章都以阶乘作为递归的入门，本篇也不能免俗。

例如!5 = 1 * 2 * 3 * 4 * 5

在数学上可以定义为：

通过数学公式，我们可以通过代码简单的转换一下，

int fact(int n) {
    if (n == 1) return 1;
    return n * fact(n - 1);
}

在fact()函数中，如果n=1，那么return 1，否则return n * fact(n - 1)。

调用过程

为了让过程更清晰，我们从头到尾看一下函数递归调用的详细过程。

1. 调用 fact(5)，进入函数：
   • 判断 5 == 1 失败，调用 fact(4)，即执行 return 5 * fact(4)。
2. 调用 fact(4)，进入函数：
   • 判断 4 == 1 失败，调用 fact(3)，即执行 return 4 * fact(3)。
3. 调用 fact(3)，进入函数：
   • 判断 3 == 1 失败，调用 fact(2)，即执行 return 3 * fact(2)。
4. 调用 fact(2)，进入函数：
   • 判断 2 == 1 失败，调用 fact(1)，即执行 return 2 * fact(1)。
5. 调用 fact(1)，进入函数：
   • 判断 1 == 1 成立，返回 1。
6. 返回到 fact(2)：
   • 执行 return 2 * 1 = 2，返回 2。
7. 返回到 fact(3)：
   • 执行 return 3 * 2 = 6，返回 6。
8. 返回到 fact(4)：
   • 执行 return 4 * 6 = 24，返回 24。
9. 返回到 fact(5)：
   • 执行 return 5 * 24 = 120，返回 120。

还是看不懂？我们来看看fact()函数的具体运算过程:

当fact() 传参为5时，n不等于1，因此返回n * fact(n - 1),也就是5 * fact(4)

当程序运行时发现fact(5)中需要计算fact(4)，因此程序会先准备执行fact(4)，那么我们看一眼fact(4)的运算过程：

n为4，因此不等于1，返回4 * fact(3)

以此类推，程序需要继续计算fact(3)、fact(2)……直到fact(1)

fact(1)传入的参数为1，因此返回 1

当程序体发现返回的参数中不需要继续计算，将直接逐层传出，从1开始往回填充对应函数的值，把fact(2)程序中的fact(1)替换为1，

fact(2)中return的是2 * 1，那么将fac(2) 为 2这个值填充给fac(3)…以此类推，层层传出到fact(5)

可以很容易发现从fact(1)返回的fact(5)的过程转化为计算步骤是：1 * 2 * 3 * 4 * 5，正是!5的计算过程

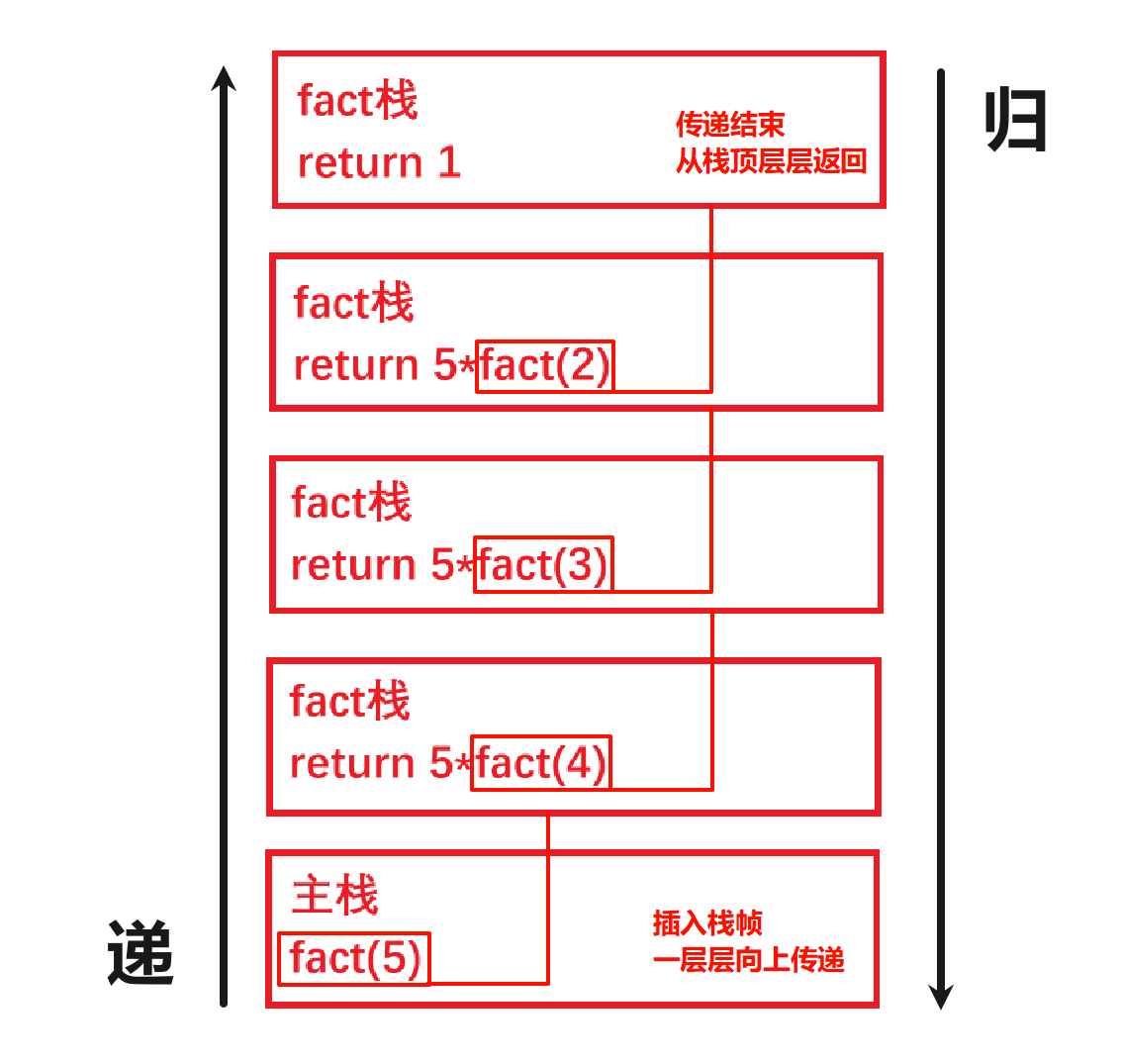
栈动作

在调用 fact(5) 时，递归函数 fact 会依次调用自身，直到满足终止条件 n == 1。每次函数调用都会在栈上创建一个新的栈帧，保存当前函数的局部变量和返回地址。当递归调用完成后，栈帧会被弹出，程序返回到上一个调用点。

汉诺塔的递归实现

汉诺塔问题的目标是将所有的盘子从起始柱移动到目标柱，但由于受到以下两条规则的限制，直接移动并不简单：

1. 每次盘子移动次数只有一次
2. 小盘子永远在大盘子上面

为了突破这些限制，汉诺塔的规则中引入了一个辅助柱作为中转站，使得从起始柱到目标柱的移动成为可能。

有了以上的核心思想后，我们要思考如何利用递归来实现。

递归的思想

前面提到过，递归的特性可以使得解决问题时将一个大问题被分解成若干个同样流程的小问题来实现。显著的简化了某些具有重复子问题结构的任务的实现方法，那么我们就要思考，汉诺塔的解题步骤中有哪些是具有重复的子流程和操作的地方呢？

我们来看一眼hanoi(3)，即初始状态下有三层的盘子的移动步骤：

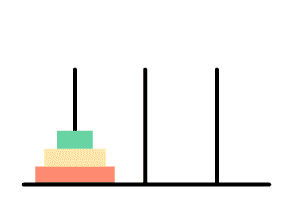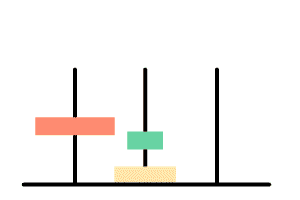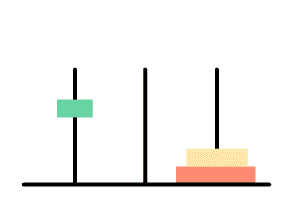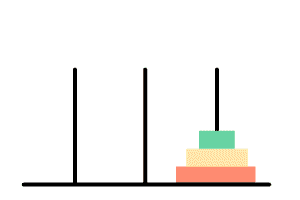
三个柱子我们将其命名为ABC，那么它的移动步骤是：

A --> C
A --> B
C --> B
A --> C
B --> A
B --> C
A --> C

注意到了吗？

想要完成目标，需要先把红盘放入c；

想要将红盘放入c，需要先把绿黄盘放入b；

想要完成把绿黄盘放入b，需要先把黄盘放入b；

想要把黄盘放入b，就需要先把绿盘放入c；

他们有着共同点，都需要先把上面的盘子解决掉，才能让下面的盘子移动。

这是不是符合了我们之前提到的具有重复子问题结构的任务？

那么你可能会觉得，每个盘放的位置又是a又是b的，虽然都在移动，但移动的起始位置与结束位置哪有共同点可言？

确实，ABC看着又乱又不好理解，我们换一个思路，不要ABC三个柱子，只分成起始柱，终点柱与辅助柱。

起始柱只是你想要移动的盘子所在的柱子

终点柱只是你想要移动的盘子要去的柱子

辅助柱则是第三个额外的柱子

这三个柱子可能是A、B、C任意柱，不要搞混了。（如果感觉还是容易搞混就把ABC柱子的概念抛弃掉）

当我们这么定义三个柱子的时候，我们再来看步骤，会发现一切都变了：

想要把红盘放入终点柱，我们需要把绿黄盘放入辅助柱。

那么绿黄盘放入辅助柱就是我们现阶段需要完成的操作，此时对红盘而言的辅助柱对黄绿盘而言就是终点柱，因此：

想要把绿黄盘放入终点柱，我们需要把绿盘放入辅助柱（这里的终点柱指的是红盘的话中的辅助柱）

到了绿盘，没有比绿盘更小的盘的，因此只需要放，没有什么前提条件了

把绿盘放入终点柱这里的终点柱指的是黄绿盘话中的辅助柱

这样看，共同点不都来了？

盘子想要放到终点柱，需要将上面的盘子放到辅助柱

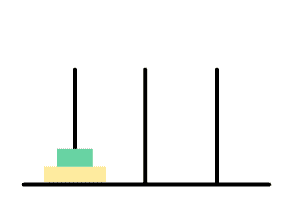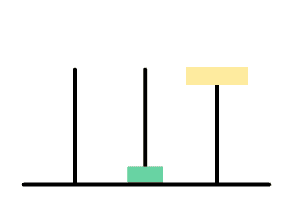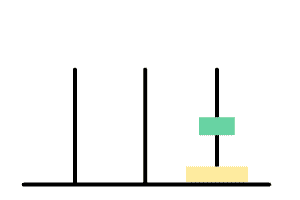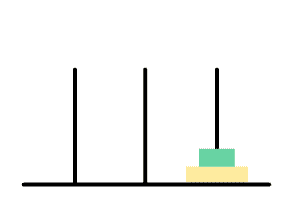
黄盘想要放到右边，需要将绿盘放到辅助柱上后黄盘移动，最后绿盘放到黄盘上即可

直到盘子剩下最后一个，此时只需要将盘子放到终点柱就好了。

这就是汉诺塔的共同点。

递归的编写

我们通过共同点将其转化为代码则是

void hanoi(int n, char source, char target, char auxiliary) {
    # 盘子只剩1个时
    if (n == 1) {
        printf("%c-->%c\n", source, target);
        return;
    }
    # 盘子为多个时
    else{
        hanoi(n - 1, source, auxiliary, target);
    	printf("%c-->%c\n", source, target);
    	hanoi(n - 1, auxiliary, target, source);
    } 
}

其中，n是盘子的数量，soure是起始柱，target是终点柱，auxiliary是辅助柱

当盘子为一个时，将起始柱的盘移到终点柱即可

当盘子为多个时，则需要将起始柱上方的盘子(也就是n-1的盘子)移动到辅助柱，即

hanoi(n - 1, source, auxiliary, target);

在这里auxiliary 和 target 的位置发生了交换——这是因为 n-1 的盘子在当前视角中要移到辅助柱，而目标柱在此时变成了辅助的角色。

紧接着第n个盘子(也就是n的盘子)移动到目标柱，即

printf("%c-->%c\n", source, target);

最后在将**辅助柱上的盘子n-1**移到目标柱的盘子n上，即

hanoi(n - 1, auxiliary, target, source);

这样整段代码就完成了，如果是python则更简洁：

def hanoi(n,source,target,auxiliary):
    if n == 1:
        print(source,'-->',target)
    else:
        hanoi(n-1,source,auxiliary,target)	# n-1移到辅助柱
        print(source,'-->',target)	# n移到目标柱
        hanoi(n-1,auxiliary,target,source)	# n-1从 辅助盘移到目标柱

这下更方便看了吧？

技巧

模拟视角来编写递归

有些人可能觉得在hanoi()函数中source,target,auxiliary三个形参要来回换很令人头大。其实，换个思路理解可能会让你更轻松：

递归时要以当前函数的视角来看问题

我们用python的代码来讲解吧，方便理解（

想象你自己是当前的第 n 个盘子，那么上一个盘子就是 n-1，如果需要的话，下一个盘子是 n+1。以此为基础，在递归编写时你就能更好地理解每一步的含义。

我们要以当前函数的视角来理解，n 这个盘子要移动到目标柱子，而在它的视角中，n-1 需要先移动到辅助柱。于是我们可以这么写：
hanoi(n-1,source,auxiliary,target) # n-1移到辅助柱

在这段代码中，n-1 代表了在当前视角中你上方的盘子，需要将其先移到辅助柱，这样才能腾出空间把 n 移动到目标柱。

然后，最后一步是将 n-1 移动到目标柱。此时，在你的视角中，n-1 则需要从辅助柱移到目标柱，即

hanoi(n-1,auxiliary,target,source) # n-1从 辅助盘移到目标柱

绝对的信任

正常编写代码是线性的，我们很容易根据业务流程或者在我们想象中程序执行顺序来进行编写。

但是递归不一样，它是以最外层开始，编写代码时从外到内，但具体的代码执行流程却是从内到外，我们很难去想象这种流程，在阅读代码也很难去想到具体的过程。

我们不要去跟踪执行的过程，而是假定这个代码我们已经写好了、已经实现了我们所想象的要求，最后再去编写代码。

这种感觉类似于调用官方函数库的感觉，完全信任它会按照我们预期的方式工作，不会去追究其内部的代码实现，在编写递归时也是，调用本身的时候要有绝对的信心——”它已经实现了我需要的正确功能，是一个能够正常使用的函数“的样子去大胆的使用，就像我们相信标准库中的函数一样，不需要过多担心其实现细节。

以上。